Le carré Un carré est un quadrilatère qui a quatre angles droits et quatre côtés égaux.
Comment faire un carré sans équerre ? Construire un carré avec le compas seulement (sans équerre ni règle graduée) Trace une droite passant par deux points. Trace deux cercles utilisant ces deux points comme centres. Ils sont représentés en bleu sur la construction.
Comment déterminer la nature d'un quadrilatère ABCD ?
- Ses côtés opposés sont parallèles deux à deux.
- Ses diagonales se coupent en leur milieu.
- Ses côtés opposés sont égaux.
- Deux côtés opposés parallèles et égaux.
Quelle est la nature du quadrilatère ABCD justifier ? Le quadrilatère ABCD est un rectangle.
Comment démontrer qu'un quadrilatère est rectangle ?
Dans le quadrilatère ABCD, les diagonales ont le même milieu O et ont la même longueur. On admettra la propriété suivante : Propriété 7 : Si un quadrilatère a ses diagonales qui ont le même milieu et la même longueur, alors ce quadrilatère est un rectangle. Comment prouver que ABCD est un losange ?
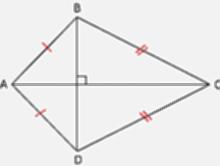
- ont le même milieu : O est le milieu de [AC] et [BD] ;
- sont perpendiculaires : (AC) perp (BD) ;
- sont les deux axes de symétrie du losange.
Comment démontrer qu'un quadrilatère est un carré avec les vecteurs ?
Application. Si deux côtés consécutifs d'un parallélogramme sont à la fois perpendiculaires et de même longueur, ou si ses diagonales sont à la fois perpendiculaires et de même longueur, alors on peut dire que c'est un carré. C'est quoi deux vecteurs colinéaires ? On dit que deux vecteurs sont colinéaires si, en multipliant les composantes de l'un des vecteurs par un scalaire k (constante), on obtient les composantes de l'autre vecteur. Donc, si le vecteur →u est colinéaire au vecteur →v , alors il existe un scalaire k tel que →u=k→v u → = k v → .
Quelle est la formule d'un parallélogramme ?
L'aire d'un parallélogramme est égale à : côté × hauteur. Donc aire (ABEF) = 6 × 3. 2. Quels sont les noms des quadrilatères ? Lister les 7 quadrilatères (sans spécifier leurs propriétés qui seront rappelées et utilisées lors de la preuve) : carré, cerf volant, fer de lance, losange, parallélogramme, rectangle, trapèze.
